Area of Equilateral Triangle: The Area of the Equilateral Triangle is quite an important topic for solving mathematics problems formulas, especially in the calculation of the space occupied between the sides of the equilateral triangle in a 2D plane. In an equilateral triangle, median, angle bisector and altitude for all sides are all the same and are the lines of symmetry of the equilateral triangle. Finding the area of an equilateral triangle is quite an easy calculation. In this article, we have discussed the area of the equilateral triangle formula, its deviation, and much more about the Area of the Equilateral Triangle.
We all know what a triangle is, it is categorised into three types: scalene triangles, equilateral triangles, and isosceles triangles.
• A scalene triangle has no equal sides or angles.
• Two sides of an isosceles triangle are equal, as are the opposing angles of equal sides.
Area of an Equilateral Triangle
The area of an equilateral triangle is the amount of space that the triangle takes up on a two- dimensional plane. We all know that the simplest form of a regular polygon is a triangle, and the term “triangle” comes from the fact that it contains three angles generated by uniting three-line segments end to end. A triangle is a closed geometric object with three angles, three sides, and three vertices. And the sum of the three angles of a triangle equals 180°. The length of the sides of a triangle determines its type.

This triangle has three equal sides and is hence known as an equilateral triangle. As a result,
each equilateral triangle angle is 60 degrees.
Area of Equilateral Triangle Formula
The formula for the area of an equilateral triangle (A) is given below,
A = (√3/4)a²
Where a is the length of the sides of an equilateral triangle.
To find the area of the Equilateral Triangle, you must know the measure of the side length of the equilateral triangle.
Apply the formula to calculate the equilateral triangle’s area given as, A = (√3/4)a², where, a is the measure of the side length of the equilateral triangle.
What is an equilateral triangle?
Yes, in simple words, an equilateral triangle is a triangle with three equal sides and three interior angles that each measure 60 degrees.
Other Equilateral Triangle Properties are:
• The perimeter of an equilateral triangle is 3s. Where ‘s’ is the equilateral triangle’s side.
• The ortho-centre and centroid of the triangle are at the same point.
• In an equilateral triangle: the median, angle bisector, and perpendicular are all identical.
Derivation of Area of the Equilateral Triangle
Let’s derive the Area of the Equilateral Triangle
We are all familiar with the primary area formula for triangles that is,
Area of Triangle = 1⁄2 × height of the triangle × base of the triangle …. (i)
Here, height = h and base = a
By using this formula, we can easily calculate the area of an equilateral triangle.
Now let us consider an equilateral triangle with sides(a) and height(h)
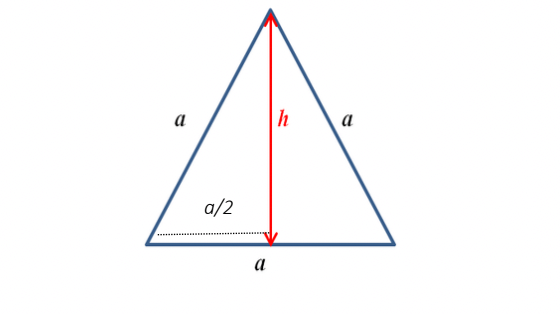
By using Pythagoras’ Theorem in the triangle, we get
H² = P² + B² …. (ii)
By putting the values in equation(ii) according to the diagram we get
a² = h² + (a / 2)²
h² = a² – (a² / 4)
h² = (3a² / 4)
h = ½ (√3a)
Now, put the value of “h” in equation (i)
Area of Triangle = 1⁄2 × height of the triangle × base of the triangle
S = ½ x ½ (√3a) x a
Area of Equilateral Triangle = ¼ (√3a²)
The perimeter of an Equilateral Triangle
Because all sides of an equilateral triangle are equal, the perimeter of an equilateral triangle equals the sum of all sides or three times of a side.
The perimeter of an Equilateral Triangle = 3a,
where a is the side
we can also remember:
• Semi Perimeter of an Equilateral Triangle = 3a/2
- • Height of an Equilateral Triangle = √3a/2


